첫째는 SelectionSort, 선택 정렬이다.


원리

1. 0부터 끝요소까지 반복한다.( current < N )

2. 현재요소( current )와 나머지 요소 중 가장 작은 값을 비교하여 더 작다면 교환이 일어난다.



특징

1. 가장 작은 값을 찾는 과정에서 비교는 여러번 일어나지만 실제로 교환은 한번만 일어 나므로 범위가 작을경우 유리하다.

2. 데이터양이 큰 경우 매번 작은 값을 찾기 때문에 매우 느리다.


연산시간

1. 최선의 경우 비교횟수 : N - 1 ( 정렬이 이미 되어 있는 경우 )

2. 최악의 경우 비교횟수 :N * (N - 1) / 2 ( 역순으로 정렬되어 있는 경우 )

- 처음에는 가장 작은 값을 찾기위해 (N - 1) 번 비교할 것이며 하나씩 정렬 될 때마다 -1 씩 하여 끝에는 1번 비교하게 될 것이다. 

즉, 비교횟수는 [ (N - 1) + (N - 2) + (N - 3) ... 1 ]이다. 

식으로 나타내면 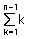  = n(n-1) / 2 이며 O표기법으로는 O(n^2)이 된다.


코드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
//SELECTIONSORT
 
void SelectionSort(int* array, int size)
{
    for (int i = 0; i < size; i++)         // i == (0 ~ size)
    {
        for (int j = i; j < size; j++){    // j == (i ~ size)
            if (array[i] > array[j])       // (i) > (j) 이면 교환
            {
                int temp = array[i];
                array[i] = array[j];
                array[j] = temp;
            }
        }
    }
}
int const MAX = 5;                        // Max 값
int g_arr[MAX] = { 0, };                  // 배열 초기화
int main()
{
    printf("========정렬전========\n");
    //AscendingNumber(g_arr, MAX);        // 순열 배열 생성
    //DescendingNumber(g_arr, MAX);       // 역순 배열 생성
    RandomNumber(g_arr, MAX);             // 랜덤 배열 생성
 
    PrintNumber(g_arr, MAX);             // 배열 출력
    printf("\n");
    clock_t start = clock();             // 시작 시간
    SelectionSort(g_arr, MAX);            // SelectionSort
    clock_t end = clock();                // 끝 시간
 
    printf("========정렬후========\n");
    PrintNumber(g_arr, MAX);             // 배열 출력
    printf("\nTime : %f\n", ((double)(end - start)) / CLOCKS_PER_SEC);
}
cs


결과


시간

시간은 MAX 값 100,000 을 기준으로 측정하였다.

랜덤 배열 : 31.60
역순 배열 : 19.13
순열 배열 : 13.20


결론

선택정렬은 가장 직관적인 정렬인것 같다. (최소값을 앞에 정렬하는 것이기 때문)

또 10000개 이하 개수에 대해서는 비교하는 것에 비해 교환횟수가 적기 때문에 빠른 속도를 나타낸다.(10000개 기준 0.64초)

하지만 O(n^2)의 알고리즘 답게 요소가 많아질 수록 응답 시간이 길어지는 것이 확실히 보인다.

'All > Algorithm' 카테고리의 다른 글

InsertionSort  (0) 2016.01.03
BubbleSort  (0) 2016.01.02
Sort Algorithm  (0) 2015.12.28
JUMPGAME_알고리즘  (0) 2015.12.28
JUMPGAME_문제  (0) 2015.12.28

최근 정렬알고리즘을 공부하면서 STL의 함수와 내가 구현한 알고리즘의 엄청난 속도차이를 느꼈다.
결론부터 말하자면 STL의 알고리즘을 분석하고 나만의 HSort를 구현하는 것이 목표이다.
HSort구현에 앞서 기존의 알고리즘들을 구현해보고 비교 분석해보았다. 
결과는 아래와 같다.(오름차순 정렬을 기준으로 비교하였다.)


전체 크기

100,000

초기 상태

난수 

역순 

이미 정렬된 상태

Insertion Sort

10.60

18.70 

0.00056

Bubble Sort

33.80

22.30 

17.60

 Selection Sort

31.60

19.13

13.20

Shell Sort 

0.036

0.012

0.0074

 Quick Sort_ver_1

 0.017

12.89

13.21

 Quick Sort_ver_2

 0.017

0.0076

0.0072

 Quick Sort_ver_3

 0.018

25.05 

 37.21

  STL::qsort

0.019

0.005

0.0008

 STL::sort

0.021

  0.0031 

 0.002

 STL::stable_sort 

0.05

0.07

 0.01 


전체 크기

100,000,000

초기 상태

난수

역순

이미 정렬된 상태

 Shell Sort

105

17 

13.6 

 Quick Sort_ver_1

23

 ( 너무 오래걸림 )

( 너무 오래걸림 )

 Quick Sort_ver_2

25

 8.98

  8.46

 Quick Sort_ver_3

32

 ( 너무 오래걸림 )

( 너무 오래걸림 )

 STL::qsort

4.40

24.20 

 0.89 

 STL::sort

0.28

8.30

1.02

STL::stable_sort 

63.01

57.23

20.57


각각의 구현된 알고리즘 및 분석 내용은 링크를 걸겠다.


추가

2015/12/28 - 비주얼스튜디오에서는 실행시간이 많이 차이난다. 특히 <algorithm>의 sort는 함수 구현이 완전 다른듯 하다. 이유는 모르겠다. 참고로 위의 시간은 맥OS의 Xcode에서 실행한 결과이다. 윈도우에서 전반적으로 시간이 느려졌으니 내컴퓨터의 성능 문제라고 할수 있겠지만 stl qsort의 경우 오히려 10, 10, 9의 시간으로 역순일때 더빠른 속도를 냈기 때문에 STL함수는 구현이 다르다고 할수 있을 것 같다.

'All > Algorithm' 카테고리의 다른 글

BubbleSort  (0) 2016.01.02
SelectionSort  (0) 2016.01.02
JUMPGAME_알고리즘  (0) 2015.12.28
JUMPGAME_문제  (0) 2015.12.28
FIBONACCI_알고리즘  (0) 2015.12.28

1. 무식하게 풀기


생각

1단계. 문제는 (0, 0)에서 시작하여 (n-1, n-1) 까지 도달할 수 있는가 이다. 함수 jump를 정의 한다.

2단계. jump(y, x) 는 (y, x)좌표에서 시작해 끝까지 갈 수 있는지 반환하는 함수다.

3단계. (y, x)를 입력받은 함수는 오른쪽으로 가는 루트와 아래로가는 루트가 존재한다.

이를 점화식으로 나타내면 아래와같다.

- jump(y + m, x) || jump(y, x + m) m = 각 보드판의 숫자


코드 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
// JUMPGAME_1
#include <iostream>
const int MAX = 101;
int g_JumpArray[MAX][MAX];
int g_BoardSize = 0;
 
// y, x의 좌표에서 끝까지 갈 수있는지를 반환하는 함수
int jump(int y, int x)
{
    // 기저사례1. y 또는 x 가 범위를 벗어났을때
    if (y >= g_BoardSize || y < 0) return 0;
    if (x >= g_BoardSize || x < 0) return 0;
    
    // 기저사례2. y와 x가 끝에 다달았을 때
    if (y == g_BoardSize - 1 && x == g_BoardSize - 1) return 1;
    
    // 여기에서 답을 계산한다.
    int value = g_JumpArray[y][x];
    // 점화식 : 갈수 있는 법 = (y + v, x) || (y, x + v)
    return (jump(y + value, x) || jump(y, x + value));
}
int main()
{
    // 테스트 케이스
    int testCase = 0;
    scanf("%d", &testCase);
    
    while(testCase--){
        // 보드판 크기 N * N
        scanf("%d", &g_BoardSize);
        
        // 보드판 입력
        for(int y = 0; y < g_BoardSize; y++)
        {
            for(int x = 0; x < g_BoardSize; x++)
            {
                scanf("%d", &g_JumpArray[y][x]);
            }
        }
        // 끝까지 도달 가능하다면 YES
        if(jump(0, 0))
            printf("YES\n");
        else
            printf("NO\n");
    }
    return 0;
}
cs

 

결과

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
2
7
1 1 1 1 1 1 1
1 1 1 1 1 1 1
1 1 1 1 1 1 1
1 1 1 1 1 1 1
1 1 1 1 1 1 1
1 1 1 1 1 1 2
1 1 1 1 1 2 0
NO
5
1 1 1 1 1 
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 0
YES
cs


결과는 나왔지만 다음과 같은 경우에 완전탐색알고리즘은 매우 오랜시간이 걸린다.

S  1  1  1  1  1

1  1  1  1  1  1

1  1  1  1  1  1

1  1  1  1  1  1

1  1  1  1  1  2

1  1  1  1  2  E


완전 탐색의 경우 모든 경로를 탐색한 후에서야 끝으로 갈 수 없다는 것을 알 것이다.

이 과정에서 같은 경로를 몇번이나 다시 탐색할 것이고 그로인해 속도저하의 결과를 가져올 것이다.



2. 메모이제이션 적용하기(기록하기)


생각

1단계. 위의 방법에서 구현했던 함수는 입력이 (y, x)로 정해져있으면 거기서 끝까지 갈 수 있는지 없는지 는 항상 일정한참조적 투명한 함수 이다. 때문에 메모이제이션을 적용하면 같은 루트를 두번이상 계산하지 않아 속도를 향상 시킬 수 있다.


코드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
// JUMPGAME_2
#include <iostream>
const int MAX = 101;
int g_JumpArray[MAX][MAX];
int g_Cache[MAX][MAX];
int g_BoardSize = 0;
 
// y, x의 좌표에서 끝까지 갈 수있는지를 반환하는 함수
int jump(int y, int x)
{
    // 기저사례1. y 또는 x 가 범위를 벗어났을때
    if (y >= g_BoardSize || y < 0) return 0;
    if (x >= g_BoardSize || x < 0) return 0;
    
    // 기저사례2. y와 x가 끝에 다달았을 때
    if (y == g_BoardSize - 1 && x == g_BoardSize - 1) return 1;
    
    // 캐시가 -1이 아니라면 캐시에 저장된 값 리턴
    int& ret = g_Cache[y][x];
    if (ret != -1) return ret;
    
    // 여기에서 답을 계산한다.
    int value = g_JumpArray[y][x];
    
    // 점화식 : 갈수 있는 법 = (y + v, x) || (y, x + v)
    ret = (jump(y + value, x) || jump(y, x + value)); //점화식
    return ret;
}
 
int main()
{
    // 테스트 케이스
    int testCase = 0;
    scanf("%d", &testCase);
    
    while(testCase--){
        // 보드판 크기 N * N
        scanf("%d", &g_BoardSize);
        
        // 보드판 입력
        for(int y = 0; y < g_BoardSize; y++)
        {
            for(int x = 0; x < g_BoardSize; x++)
            {
                scanf("%d", &g_JumpArray[y][x]);
            }
        }
        // 캐시 배열 초기화
        memset(g_Cache, -1, sizeof(g_Cache));
        
        // 끝까지 도달 가능하다면 YES
        if(jump(0, 0))
            printf("YES\n");
        else
            printf("NO\n");
    }
    return 0;
}
cs

 

결과


결과는 위의 것과 같다.


캐시를 사용하여 한번 계산한 루트에 대한 값을 저장하고 있다가 그부분에 대한 계산을 요구할 시 캐시값을 반환하는 형태로 수정하였다.

N이 커질수록 메모이제이션을 적용한 것과 안한 것의 속도차이가 커지는 것을 확인 할 수 있다.

'All > Algorithm' 카테고리의 다른 글

SelectionSort  (0) 2016.01.02
Sort Algorithm  (0) 2015.12.28
JUMPGAME_문제  (0) 2015.12.28
FIBONACCI_알고리즘  (0) 2015.12.28
FIBONACCI_문제  (0) 2015.12.28

문제

 

땅따먹기를 하다 질린 재하와 영훈이는 땅따먹기의 변종인 새로운 게임을 하기로 했습니다. 이 게임은 그림과 같이 n*n 크기의 격자에 각 1부터 9 사이의 정수를 쓴 상태로 시작합니다. 각 차례인 사람은 맨 왼쪽 윗 칸에서 시작해 외발로 뛰어서 오른쪽 아래 칸으로 내려가야 합니다. 이 때 각 칸에 적혀 있는 숫자만큼 오른쪽이나 아래 칸으로 움직일 수 있으며, 중간에 게임판 밖으로 벗어나면 안 됩니다.

균형을 잃어서 다른 발로 서거나 넘어져도 게임에서 집니다만, 재하와 영훈이는 젊고 활기차기 때문에 외발로 뛰어다니는 것은 아무것도 아닙니다. 다만 걱정되는 것은 주어진 게임판에 시작점에서 끝점으로 가는 방법이 존재하지 않을 수도 있다는 것입니다. 예를 들어 그림 (a)의 게임판에서는 사각형으로 표시된 칸들을 통해 끝에 도달할 수 있지만, 숫자가 하나 바뀐 그림 (b)에서는 그럴 수가 없습니다.

게임판이 주어질 때 왼쪽 위의 시작점에서 오른쪽 아래의 시작점에 도달할 수 있는 방법이 있는지 확인하는 프로그램을 작성하세요.

 

입력

 

입력의 첫 줄에는 테스트 케이스의 수 C(C <= 50)가 주어집니다. 각 테스트 케이스의 첫 줄에는 격자의 크기 n(2 <= n <= 100)이 주어지고, 그 후 n줄에 각 n개의 숫자로 왼쪽 위부터 각 칸에 쓰인 숫자들이 주어집니다. 오른쪽 아래 있는 끝 점 위치에는 0이 주어집니다.

 

출력

 

각 테스트 케이스마다 한 줄로, 시작점에서 끝 점으로 도달할 수 있을 경우 "YES"를, 아닐 경우 "NO"를 출력합니다. (따옴표 제외)

 

예제 입력

2
7
2 5 1 6 1 4 1
6 1 1 2 2 9 3
7 2 3 2 1 3 1
1 1 3 1 7 1 2
4 1 2 3 4 1 2
3 3 1 2 3 4 1
1 5 2 9 4 7 0
7
2 5 1 6 1 4 1
6 1 1 2 2 9 3
7 2 3 2 1 3 1
1 1 3 1 7 1 2
4 1 2 3 4 1 3
3 3 1 2 3 4 1
1 5 2 9 4 7 0

예제 출력

YES
NO
문제출저 : 알고스팟


'All > Algorithm' 카테고리의 다른 글

Sort Algorithm  (0) 2015.12.28
JUMPGAME_알고리즘  (0) 2015.12.28
FIBONACCI_알고리즘  (0) 2015.12.28
FIBONACCI_문제  (0) 2015.12.28
BOGGLEGAME_알고리즘_3  (0) 2015.12.28

1. 점화식을 이용한 일반적인 방법


생각


단계1. 먼저 피보나치 수열은 앞에서도 이야기 했지만 f(n) = f(n-1) + f(n-2)로 정의된다. 

단계2. 이 식을 점화식으로 재귀함수를 만들 수있다.

함수 내용 

 - 함수 f는 n을 입력받아 n번째 피보나치수를 리턴하는 재귀함수이다.

 - n이 2 이하 라면 1을 리턴한다..

 - n이 3 이상 이라면 f(n-1) + f(n-2)를 리턴한다.


단계3. 리턴 받은 수를 2로 나눈 나머지가 0이라면 짝수 이므로 YES, 0이 아니라면 NO를 출력한다.


코드


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <iostream>
 
// 함수 구현
// n번째 수의 피보나치 수열을 재귀적으로 반환
long long f(int n)
{
    // 기저사례 : n이 2 이하면 1반환
    if(n <= 2)
    {
        return 1;
    }
    // 점화식 f(N) = f(N-1) + f(N-2)
    return f(n-1) + f(n-2);
}
 
int main()
{
    // 테스트 케이스
    int testCase = 0;
    // 숫자 N
    int N = 0;
    scanf("%d", &testCase);
    
    while(testCase--){
        scanf("%d", &N);
        long long result = f(N);
        // 짝수면 YES
        if(result % 2 == 0)
            printf("YES\n");
        else
            printf("NO\n");
    }
}
cs

 

결과


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
10
10
NO
10
NO
10
NO
20
NO
30
YES
40
NO
50
NO
cs


답은 구했지만 위의 코드는 함수내에서 같은 함수를 2번 호출하는 재귀함수 이므로 2^n의 시간 복잡도를 가지며 매우 오랜시간이 걸린다. 




2. 캐시활용


생각


앞에서 [BOGGLEGAME_알고리즘_3] 에서 시간을 줄일때 사용했던 방법과 같은 아이디어로 시간을 절약 할 수있다.

단계1. 캐시를 저장할 수있는 배열을 정의하고 0으로 초기화한다.

단계2. 배열의  N번째 요소가 0이라는 것은 이전에 계산된적 없는 피보나치 수라는 것으로 계산하여   캐시배열에 저장한후 리턴한다.

단계3. 배열의 N번째 요소에 0이 아닌 값이 있다는 것은 한번 계산한 값이란 의미로 그 인덱스를 바로 참조하여 리턴한다.


코드


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
// FIBONACCI_2
 
#include <iostream>
 
// 캐시 저장 배열
long long g_CacheArr[1001] = {0,};
 
// 함수 구현
// n번째 수의 피보나치 수열을 재귀적으로 반환
long long f(int n)
{
    // 기저사례 : n이 2 이하면 1반환
    if(n <= 2)
    {
        return 1;
    }
    
    // 캐시의 해당 요소가 아직 계산되지 않은 값이라면
    // 캐시 배열에 점화식으로 계산한 값 저장
    if(g_CacheArr[n] == 0)
        return g_CacheArr[n] = f(n-1) + f(n-2);
    else// 해당요소가 이미 계산된 값이라면 캐시값 리턴
        return g_CacheArr[n];
}
 
int main()
{
    // 테스트 케이스
    int testCase = 0;
    // 숫자 N
    int N = 0;
    scanf("%d", &testCase);
    
    while(testCase--){
        // 캐시배열 초기화
        memset(g_CacheArr, 0, sizeof(g_CacheArr));
        scanf("%d", &N);
        long long result = f(N);
        // 짝수면 YES
        if(result % 2 == 0)
            printf("YES\n");
        else
            printf("NO\n");
    }
}
cs


결과


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
10
10
NO
20
NO
30
YES
40
NO
50
NO
60
YES
70
NO
80
NO
90
YES
1000
NO
cs

 


숫자가 작을때는 큰차이를 보이지 않지만 40이상만 넘어가더라도 매우 큰 차이를 확인 할 수있다. 

'All > Algorithm' 카테고리의 다른 글

JUMPGAME_알고리즘  (0) 2015.12.28
JUMPGAME_문제  (0) 2015.12.28
FIBONACCI_문제  (0) 2015.12.28
BOGGLEGAME_알고리즘_3  (0) 2015.12.28
BOGGLEGAME_알고리즘_2  (0) 2015.12.28
이번문제는 내가 만들었다.


문제

 

N번째 피보나치 수를 구한 후 그 수가 짝수이면 YES, 아닐경우 NO를 출력하는 프로그램을 구성하시오.

피보나치 수열이란 1  1  2  3  5  8  13  21  34  55... 으로 이어지는 수열로 N번째 피보나치수는 (N-1) + (N-2)이 됩니다.

 

입력

 

입력의 첫 줄에는 테스트 케이스의 수 C(C <= 50)가 주어집니다. 각 테스트 케이스의 첫 줄에는 N(1<= N <= 1,000)이 입력됩니다.

 

출력

 

각 테스트 케이스마다 수가 짝수일 경우 YES, 아닐 경우 NO를 출력합니다.

 

예제 입력

4
6
3
4
2



예제 출력

YES
YES
NO
NO


'All > Algorithm' 카테고리의 다른 글

JUMPGAME_문제  (0) 2015.12.28
FIBONACCI_알고리즘  (0) 2015.12.28
BOGGLEGAME_알고리즘_3  (0) 2015.12.28
BOGGLEGAME_알고리즘_2  (0) 2015.12.28
BOGGLEGAME_알고리즘_1  (0) 2015.12.28

3. 중첩으로 저장하는 부분 제외하기 


생각

기본적인 원리는 [BOGGLEGAME_알고리즘_1]과 동일하다. 

하지만 조금 깊게 생각해보면 8방향을 검사할때 중첩되는 부분이 있다는 것을 알 수 있다.

예를 들면 


0  1  2

3  4  5

6  7  8


일때 


이런식으로 갈수 있는 방향을 트리로 정리할 수 있다. 

이때 트리의 깊이가 단어의 길이라고 생각하면 붉은 원 두개가 서로 같은 정보를 가지고 있는 것을 알 수 있다. 

이 알고리즘의 핵심은 이 붉은 부분을 검사한 후 그 결과값을 저장해 놓는다는 것에 있다.

즉, 단어의 4번째 글자를 찾기 위해 재귀적으로 검사할때 

0번으로 들어가서 검사할 수 있는 위 3개(1, 3, 4)의 각 요소에 찾는 알파벳이 없다면 

더이상 4번째 글자를 찾기 위해 0번으로 들어가 일일이 확인해 볼 필요가 없다는 것이다. 


위의 아이디어를 구현하기위해 필요한 코드는 의외로 간단하다.

기존의 코드에 캐시를 저장할 수 있는 배열을 만들어놓고, 위와 같은 상황이 되면 -1로 표시하는 부분만 구현하면 된다.


코드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
// BOGGLEGAME_2
#include <iostream>
#include <string.h>
static const int BOGGLE_MAX = 5;
static const int WORD_MAX = 10;
int g_ArrX[] = { -1, 0, 1, 1, 1, 0, -1, -1 };
int g_ArrY[] = { -1, -1, -1, 0, 1, 1, 1, 0 };
char* g_Boggle[BOGGLE_MAX];
char* g_WordsArr[WORD_MAX];
// 기록 배열
char g_CacheArr[BOGGLE_MAX][BOGGLE_MAX][WORD_MAX] = {0,};
int g_StringLen = 0;
int g_CurCharNum = 0;
int g_CurWordNum = 0;
// 해당 좌표에 전달되는 문자가 있는지 검사
bool f(int y, int x, char CurChar)
{
    // 기저사례 1 x또는 y가 범위 밖이라면 false
    if (x < 0 || y < 0)
        return false;
    
    // 기저사례 1 x또는 y가 범위 밖이라면 false
    if (x >= BOGGLE_MAX || y >= BOGGLE_MAX)
        return false;
    
    // 기저사례 2 찾으려는 문자가 '\0' 이거나
    // 문자열의 길이와 같으면 문자열을 찾은것이므로 true
    if (CurChar == '\0' || g_CurCharNum > g_StringLen)
        return true;
    
    // 찾으려고 하는 좌표가 이미 -1 이라면 여긴 이전에 찾았던 곳이므로 패스
    if (g_CacheArr[y][x][g_CurCharNum] == -1)
        return false;
    
    if (g_Boggle[y][x] == CurChar)
    {
        if (g_StringLen == 1){
            // 기저사례 3 문자를 찾았는데 문자열의
            // 길이가 1이면 곧 찾는 문자열이므로 true
            return true;
        }
        // 문자를 찾았으면 문자인덱스를 1증가
        ++g_CurCharNum;
        // 현 인덱스를 중심으로 다음 문자를 8방향 검사
        for (int i = 0; i < 8; i++)
        {
            // 모두 찾으면 true
            if (f(
                  (y + g_ArrY[i]), // y좌표
                  (x + g_ArrX[i]), // x좌표
                  g_WordsArr[g_CurWordNum][g_CurCharNum])
                )
            {
                return true;
            }
        }
        // 문자를 못찾았으면 문자인덱스 1감소
        --g_CurCharNum;
        
        // 8방향 모두 아니라면 현재 좌표에서 다음문자를 찾을 방법이 없기때문에 -1
        g_CacheArr[y][x][g_CurCharNum] = -1;
    }
    // 현 인덱스의 문자가 찾는 문자가 아니면 false
    return false;
}
 
int main()
{
    // 테스트 케이스
    int testCase = 0;
    int stringCount = 0;
    int temp = 0;
    for (int i = 0; i < BOGGLE_MAX; i++)
    {
        g_Boggle[i] = new char[BOGGLE_MAX + 1]();
    }
    for (int i = 0; i < WORD_MAX; i++)
    {
        g_WordsArr[i] = new char[WORD_MAX + 1]();
    }
    scanf("%d", &testCase);
    while (testCase--){
        g_CurWordNum = 0;
        
        // 보글게임판 5 x 5 입력
        for (int i = 0; i < BOGGLE_MAX; i++)
        {
            scanf("%s", g_Boggle[i]);
        }
        // 확인하려는 문자열 갯수 입력
        scanf("%d", &stringCount);
        temp = stringCount;
        // 확인하려는 문자열 입력  ENTER 구분
        for (int i = 0; i < stringCount; i++)
           {
            scanf("%s", g_WordsArr[i]);
        }
        while (stringCount--){
            bool isYes = false;
            // 단어를 찾는 루프를 돌 때마다 캐시를 -1로 초기화해준다.
            memset(g_CacheArr, 0, sizeof(g_CacheArr));
            // 현재 검사하려고 하는 문자열의 길이 저장
            g_StringLen = (int)strlen((const char*)g_WordsArr[g_CurWordNum]);
            // g_CurCharNum = 현재 검사하려고하는 문자 인덱스 예) ABCDE에서 C 면 2
            g_CurCharNum = 0;
            for (int y = 0; y < BOGGLE_MAX; y++)
            {
                for (int x = 0; x < BOGGLE_MAX; x++)
                {
                    // y, x인덱스와 찾으려는 문자열의 문자를 f에 넘김
                    // 있으면 YES
                    if (
                        f(y,
                          x,
                          g_WordsArr[g_CurWordNum][g_CurCharNum]))
                    {
                        printf("%s YES\n", g_WordsArr[g_CurWordNum++]);
                        isYes = true;      // 루프를 빠져나간다.
                        break;              // 루프를 빠져나간다.
                    }
                }
                if (isYes)               // 루프를 빠져나간다..
                    break;                   // 루프를 빠져나간다..
            }
            
            // 4, 4까지 돌았는데 없으면 NO
            if (!isYes)
            {
                printf("%s NO\n", g_WordsArr[g_CurWordNum++]);
            }
        }
    }
    
    // 메모리 해제
    for (int i = 0; i < BOGGLE_MAX; i++)
    {
        delete []g_Boggle[i];
        g_Boggle[i] = NULL;
    }
    for (int i = 0; i < WORD_MAX; i++)
    {
        delete[]g_WordsArr[i];
        g_WordsArr[i] = NULL;
    }
    return 0;
}
cs

총 4곳이 수정되었다.(main 1 + 함수 3)


1. 첫번째는 캐시 배열을 선언하는 부분

1
2
// 캐시 배열
char g_CacheArr[BOGGLE_MAX][BOGGLE_MAX][WORD_MAX] = {0,};
cs


2. 둘째는 현재 좌표가 -1(이전에 찾아본 곳)일 경우 false를 반환하는 부분

1
2
3
// 찾으려고 하는 좌표가 이미 -1 이라면 여긴 이전에 찾았던 곳이므로 패스
if (g_CacheArr[y][x][g_CurCharNum] == -1)
    return false;
cs


3. 셋째는 8방향이 모두 아니라면 -1로 마킹하는 부분이다.

1
2
// 8방향 모두 아니라면 현재 좌표에서 다음문자를 찾을 방법이 없기때문에 -1
g_CacheArr[y][x][g_CurCharNum] = -1;
cs


4. 넷째는 캐시 배열을 초기화 하는 부분이다.(main)

while(StringCount--) 이후에 추가된다.

1
2
// 단어를 찾는 루프를 돌 때마다 캐시를 -1로 초기화해준다.
memset(g_CacheArr, 0, sizeof(g_CacheArr));
cs



결과


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
1
AAAAA
AAAAA
AAAAA
AAAAA
AAAAA
5
AAAAAAAAAAD
AAAAAAAAAAD
AAAAAAAAAAD
AAAAAAAAAAD
AAAAAAD
AAAAAAAAAAD NO
AAAAAAAAAAD NO
AAAAAAAAAAD NO
AAAAAAAAAAD NO
AAAAAAD NO
cs


이로써  BOGGLEGAME문제를 해결할 수 있었다. 

시간은 6ms가 나왔다.



'All > Algorithm' 카테고리의 다른 글

FIBONACCI_알고리즘  (0) 2015.12.28
FIBONACCI_문제  (0) 2015.12.28
BOGGLEGAME_알고리즘_2  (0) 2015.12.28
BOGGLEGAME_알고리즘_1  (0) 2015.12.28
BOGGLEGAME_문제  (0) 2015.12.28

2. 배열에 표시하기


생각

1단계. 25 x 25의 배열 선언

2단계. 각 원소에 인접함의 유무를 저장함

ex) 4 x 4 일때


A  A  A  S     ->        0   1   2   3

A  E  E  A     ->        4   5   6   7

A  Y  E  A     ->        8   9  10  11

A  A  A  A     ->       12  13  14 15

이면 


arr[15][15] = 

    0  1  2  3  4  5  6  7  8  9  10  11  12  13  14  15

0      1          4  5 

1  0      2      4  5  6

2      1      3      5  6  7

3          2              6  7

4  0  1              5          8  9

5  0  1  2      4      6      8  9  10

6      1  2  3      5      7      9  10  11

7          2  3          6              10  11

8                  4  5              9              12  13

9                  4  5  6      8      10        12  13  14

10                    5  6  7      9        11        13  14  15

11                        6  7          10                    14  15

12                                8  9                    13

13                                8  9  10        12        14

14                                    9  10  11        13        15

15                                        10  11              14


3단계. 찾고자하는 문자열을 위의 인덱스로 변환후 저장한다.

ex) YES -> 9 6 3

      YEA -> 9 10 11

4단계. 저장한 숫자 배열(편의상 YES배열 )을 순회하며 arr[ i ][ i+1 ]에 YES의 (i+1)번째 요소가 들어있는지 검사한다.  있으면 i++ 후 i가 숫자 배열의 끝일때까지 반복

ex) YES -> ( arr[YES[i] ][ YES[i+1] ] == 6) 


문제


처음 위 알고리즘을 생각했을땐 2차원 배열을 가장먼저 만들어 놓기만 하면 모든 답을 처리할수 있기에 시간적인 문제를 해결할 수 있을 것이라 생각했다. 때문에 정답이라고 생각했는데 다음과 같은 경우에 답을 찾지 못하는 문제가 있다.


A  A  A  A     ->        0   1   2   3

A  E  E  E     ->        4   5   6   7

A  Y  A  A     ->        8   9  10  11

A  A  A  A     ->       12  13  14 15


일때  E E E Y의 경우 숫자배열에 5 6 5 9 로 저장되어야 함이 맞다. 하지만 위의 알고리즘은 숫자 배열을 만들때 

8방향 탐색을 하지 않는다. 때문에 7의 E를 저장하고 다음 요소인 Y를 찾을 수 없어 오답처리된다.


다른 방법을 찾아야겠다.

'All > Algorithm' 카테고리의 다른 글

FIBONACCI_문제  (0) 2015.12.28
BOGGLEGAME_알고리즘_3  (0) 2015.12.28
BOGGLEGAME_알고리즘_1  (0) 2015.12.28
BOGGLEGAME_문제  (0) 2015.12.28
ZEROONE_알고리즘  (0) 2015.12.28

1. 무식하게 풀기


생각

1단계. 먼저 5 x 5 배열에 문자열을 입력받는다.

2단계. 그후 검사할 문자열들을 N개 입력 받는다.

3단계. 입력받은 각 문자열의 문자들이 서로 인접하고 있는지를 판단하는 함수를 호출 true면 YES, false면 NO 출력

함수 내용 

 - bool f(int x,  int y,  char curCharacter) 

 - x 또는 y가 범위 0 <= (x, y) < 5 가 아니라면 false

 - 배열의 [y][x] 인덱스에 있는 문자가 찾아야 할 문자가 아니면 false

 - 해당 인덱스의 문자가 찾는 문자이고 문자열의 길이가 1이라면 true

 - 해당 인덱스의 문자가 찾는 문자이고 문자열의 길이가 1이 아니라면 다음 문자를 인접하는 8방향의 x, y와 다음 문자를 인자로 f함수 재귀 호출

 - 찾는 문자가 문자열의 마지막 문자이면 모두 찾은 것이므로 true


코드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
// BOGGLEGAME_1
#include <iostream>
#include <string.h>
static const int BOGGLE_MAX = 5;
static const int WORD_MAX = 10;
int g_ArrX[] = { -1, 0, 1, 1, 1, 0, -1, -1 };
int g_ArrY[] = { -1, -1, -1, 0, 1, 1, 1, 0 };
char* g_Boggle[BOGGLE_MAX];
char* g_WordsArr[WORD_MAX];
int g_StringLen = 0;
int g_CurCharNum = 0;
int g_CurWordNum = 0;
 
// 해당 좌표에 전달되는 문자가 있는지 검사
bool f(int y, int x, char CurChar)
{
    // 기저사례 1 x또는 y가 범위 밖이라면 false
    if (x < 0 || y < 0)     
        return false;
    // 기저사례 1 x또는 y가 범위 밖이라면 false
    if (x >= BOGGLE_MAX || y >= BOGGLE_MAX)     
        return false;
    // 기저사례 2 찾으려는 문자가 '\0' 이거나
    // 문자열의 길이와 같으면 문자열을 찾은것이므로 true
    if (CurChar == '\0' || g_CurCharNum > g_StringLen)      
        return true;
                                             
    if (g_Boggle[y][x] == CurChar)
    {
        if (g_StringLen == 1){
            // 기저사례 3 문자를 찾았는데 문자열의 
            // 길이가 1이면 곧 찾는 문자열이므로 true
            return true;
        }
 
        // 문자를 찾았으면 문자인덱스를 1증가
        ++g_CurCharNum;   
 
        // 현 인덱스를 중심으로 다음 문자를 8방향 검사
        for (int i = 0; i < 8; i++)
        {
            // 모두 찾으면 true
            if (f(
                (y + g_ArrY[i]), // y좌표
                (x + g_ArrX[i]), // x좌표
                g_WordsArr[g_CurWordNum][g_CurCharNum])
                )
            {
                return true;       
            }
        }
        // 문자를 못찾았으면 문자인덱스 1감소
        --g_CurCharNum;      
    }
    // 현 인덱스의 문자가 찾는 문자가 아니면 false
    return false;       
}
 
 
int main()
{
    // 테스트 케이스
    int testCase = 0;
    int stringCount = 0;
    int temp = 0;
    for (int i = 0; i < BOGGLE_MAX; i++)
    {
        g_Boggle[i] = new char[BOGGLE_MAX + 1]();
    }
    for (int i = 0; i < WORD_MAX; i++)
    {
        g_WordsArr[i] = new char[WORD_MAX + 1]();
    }
 
    scanf("%d", &testCase);
    while (testCase--){
        g_CurWordNum = 0;
        
        // 보글게임판 5 x 5 입력
        for (int i = 0; i < BOGGLE_MAX; i++)     
        {
            scanf("%s", g_Boggle[i]);
        }
 
        // 확인하려는 문자열 갯수 입력
        scanf("%d", &stringCount);
        temp = stringCount;
        // 확인하려는 문자열 입력  ENTER 구분
        for (int i = 0; i < stringCount; i++)
           {
            scanf("%s", g_WordsArr[i]);
        }
 
        while (stringCount--){
            bool isYes = false;
            // 현재 검사하려고 하는 문자열의 길이 저장
            g_StringLen = (int)strlen((const char*)g_WordsArr[g_CurWordNum]);
            // g_CurCharNum = 현재 검사하려고하는 문자 인덱스 예) ABCDE에서 C 면 2    
            g_CurCharNum = 0;               
 
            for (int y = 0; y < BOGGLE_MAX; y++)
            {
                for (int x = 0; x < BOGGLE_MAX; x++)
                {
                    // y, x인덱스와 찾으려는 문자열의 문자를 f에 넘김
                    // 있으면 YES
                    if (
                        f(y,
                          x, 
                          g_WordsArr[g_CurWordNum][g_CurCharNum]))     
                    {
                        printf("%s YES\n", g_WordsArr[g_CurWordNum++]);
                        isYes = true;      // 루프를 빠져나간다.
                        break;              // 루프를 빠져나간다.
                    }
                }
                if (isYes)              // 루프를 빠져나간다..
                break;                      // 루프를 빠져나간다..
            }
            
            // 4, 4까지 돌았는데 없으면 NO    
            if (!isYes)     
            {
                printf("%s NO\n", g_WordsArr[g_CurWordNum++]);
            }
        }
    }
    
    // 메모리 해제
    for (int i = 0; i < BOGGLE_MAX; i++)        
    {
        delete []g_Boggle[i];
        g_Boggle[i] = NULL;
    }
    for (int i = 0; i < WORD_MAX; i++)
    {
        delete[]g_WordsArr[i];
        g_WordsArr[i] = NULL;
    }
    return 0;
}
cs

결과

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
1
KKKKS
KEEEK
KEYEK
KEEEK
KKKKK
10
YES
YESYES
SYESEY
YESSEY
SYESKSYEY
YESKK
SYESKKY
YESKEY
YESEEY
YESEEEEEEEY
YES YES
YESYES NO
SYESEY NO
YESSEY NO
SYESKSYEY NO
YESKK YES
SYESKKY NO
YESKEY YES
YESEEY YES
YESEEEEEEEY YES
cs


위 방법으로 구하면 최대 

50(최대 테스트 케이스) * 10(문자열의 개수)  * 8^10 (8방향으로 검사하는 것을 글자수만큼 반복 최대 10)

대략 5000억 정도..어마어마하다. 당연 시간초과

이것을 어떻게 줄일 수 있을까.

'All > Algorithm' 카테고리의 다른 글

BOGGLEGAME_알고리즘_3  (0) 2015.12.28
BOGGLEGAME_알고리즘_2  (0) 2015.12.28
BOGGLEGAME_문제  (0) 2015.12.28
ZEROONE_알고리즘  (0) 2015.12.28
ZEROONE_문제  (0) 2015.12.28

이번에 푼 문제는 BOGGLEGAME 이다.

아래와 같다.


문제

 

보글(Boggle) 게임은 그림 (a)와 같은 5x5 크기의 알파벳 격자인 
게임판의 한 글자에서 시작해서 펜을 움직이면서 만나는 글자를 그 순서대로 나열하여 만들어지는 영어 단어를 찾아내는 게임입니다. 펜은 상하좌우, 혹은 대각선으로 인접한 칸으로 이동할 수 있으며 글자를 건너뛸 수는 없습니다. 지나간 글자를 다시 지나가는 것은 가능하지만, 펜을 이동하지않고 같은 글자를 여러번 쓸 수는 없습니다.

예를 들어 그림의 (b), (c), (d)는 각각 (a)의 격자에서 PRETTY, GIRL, REPEAT을 찾아낸 결과를 보여줍니다.

보글 게임판과 알고 있는 단어들의 목록이 주어질 때, 보글 게임판에서 각 단어를 찾을 수 있는지 여부를 출력하는 프로그램을 작성하세요.

 

입력

 

입력의 첫 줄에는 테스트 케이스의 수 C(C <= 50)가 주어집니다. 각 테스트 케이스의 첫 줄에는 각 5줄에 5글자로 보글 게임판이 주어집니다. 게임판의 모든 칸은 알파벳 대문자입니다.
그 다음 줄에는 우리가 알고 있는 단어의 수 N(1 <= N <= 10)이 주어집니다. 그 후 N줄에는 한 줄에 하나씩 우리가 알고 있는 단어들이 주어집니다. 각 단어는 알파벳 대문자 1글자 이상 10글자 이하로 구성됩니다.

 

출력

 

각 테스트 케이스마다 N줄을 출력합니다. 각 줄에는 알고 있는 단어를 입력에 주어진 순서대로 출력하고, 해당 단어를 찾을 수 있을 경우 YES, 아닐 경우 NO를 출력합니다.

 

예제 입력

1
URLPM
XPRET
GIAET
XTNZY
XOQRS
6
PRETTY
GIRL
REPEAT
KARA
PANDORA
GIAZAPX

예제 출력

PRETTY YES
GIRL YES
REPEAT YES
KARA NO
PANDORA NO
GIAZAPX YES


요약하면

1. 5 x 5의 배열에 문자열 입력 

2. 그후 길이가 10이하인 문자열 N개 입력

3. 5 x 5의 배열의 한 원소에서 시작해서 인접하는 원소들을 연결하여 문자열이 존재하는지 확인 존재하면 YES 아니면 NO 

4. 연결할때 사용했던 문자를 다시 사용할 수 는 있지만 한 문자를 연속해서 계속 사용할 수는 없다.

조건 테스트케이스는 50이며 10000ms안에 수행되어야한다. 

*문제 출저 알고스팟

'All > Algorithm' 카테고리의 다른 글

BOGGLEGAME_알고리즘_3  (0) 2015.12.28
BOGGLEGAME_알고리즘_2  (0) 2015.12.28
BOGGLEGAME_알고리즘_1  (0) 2015.12.28
ZEROONE_알고리즘  (0) 2015.12.28
ZEROONE_문제  (0) 2015.12.28

+ Recent posts

티스토리툴바